| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 아파치
- 기울기
- 역전파
- AdaGrad
- 오차역전파법
- 딥러닝
- CTF
- PostgreSQL
- 백준
- Python
- HTML
- 설치
- Python Challenge
- 신경망
- Apache2
- 소프트맥스 함수
- 우분투
- flag
- sgd
- PICO CTF
- 코딩
- 파이썬
- PHP
- 순전파
- 신경망 학습
- 리뷰
- FastAPI
- C언어
- 책
- picoCTF
- Today
- Total
Story of CowHacker
딥러닝 2.1 신경망 본문
시그모이드 함수

그림 1은 시그모이드 함수를 수식으로 나타낸 것이다.
exp(-x)에서 e는 자연상 수로 2.7182... 의 값을 갖는 실수다.
시그모이드 함수 구현하기
시그모이드 함수 식 구현하기
import numpy as num
def sigmoid(x):
return 1 / ( 1 + num.exp ( -x ) )
시그모이드 함수 그래프로 구현하기
import numpy as num
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / ( 1 + num.exp ( -x ) )
x = num.arange ( -5.0, 5.0, 0.1 )
y = sigmoid ( x)
plt.plot ( x, y )
plt.ylim ( -0.1, 1.1 )
plt.show()

계단 함수 구현 하기
계단 함수 식 구현하기
import numpy as num
def step_function ( x ) :
y = x > 0
return y.astype ( num.int )
계단 함수 그래프로 구현하기
import numpy as num
import matplotlib.pyplot as plt
def step_function ( x ) :
y = x > 0
return y.astype ( num.int )
def step_function ( x ) :
return num.array ( x > 0, dtype = num.int )
x = num.arange ( -5.0, 5.0, 0.1 )
y = step_function ( x )
plt.plot ( x, y )
plt.ylim ( -0.1, 1.1 )
plt.show()

시그모이드 함수와 계단 함수의 공통점은 비선형 함수라는 점이다.
비선형 함수, 즉 퍼셉트론에서 단일 퍼셉트론과 다중 퍼셉트론 중 다중 퍼셉트론이 비선형 함수에 속한다.
직선 한 개로는 그릴 수 없는 그래프가 바로 비선형 함수다.
선형 함수는 직선 한 개로 그릴 수 있는 그래프, 즉 단일 퍼셉트론이다.
신경망에서는 바로 이 비선형 함수를 사용해야만 한다.
그 이유는 선형 함수는 층을 아무리 깊게 해도 은닉층이 없는 네트워크로도 똑같은 기능을 할 수 있기 때문이다.
먼저 선영 함수의 수식으로 표현하면
f ( x ) = ax + b
이때 a와 b는 상수다.
예를 들어보자
h ( x ) = cx를 활성화 함수로 사용한 3층 네트워크를 생각해보면,
y = ( x ) = h ( h ( h ( x ) ) )가 된다.
이 식은 y ( x ) = c * c * c * ( x )가 되는데 이건 y ( x ) = c3 ( x )와 같은 식이 된다.
결국에는 몇 층이던지 직선 그래프가 그려지기 때문에 여러 층으로 구성하는 이점을 사용할 수가 없다.
ReLU 함수
신경망에서 오랫동안 시그 모드 함수를 사용했으나,
최근 RELU 함수를 많이 사용한다.
입력이 0을 넘으면 그 입력값을 그대로 출력하고, 0 이하면 0을 출력하는 함수다.
ReLU 함수 수식
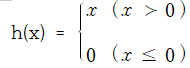
ReLU 함수 식 구현하기
import numpy as num
def relu ( x ) :
return num.maximum ( 0, x )
ReLU 함수 그래프로 구현하기
import matplotlib.pyplot as plt
import numpy as num
x = num.arange ( -5.0, 5.0, 0.1 )
y = relu(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

이로써 선형 함수와 비선형 함수의 차이점을 알았고
비선형 함수인 시그모이드 함수와 계단 함수, ReLU 함수에 대해서도 알아보았다.
'공부 > 딥러닝' 카테고리의 다른 글
| 딥러닝 2.4 신경망 (0) | 2020.08.03 |
|---|---|
| 딥러닝 2.3 신경망 (0) | 2020.08.03 |
| 딥러닝 2.2 신경망 (0) | 2020.07.26 |
| 딥러닝 2.0 신경망 (0) | 2020.07.25 |
| 딥러닝 1. 퍼셉트론 (0) | 2020.07.22 |




