| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- PostgreSQL
- PICO CTF
- 책
- 설치
- picoCTF
- 백준
- 파이썬
- C언어
- Python
- HTML
- sgd
- FastAPI
- Apache2
- 딥러닝
- Python Challenge
- 신경망
- 우분투
- 리뷰
- AdaGrad
- CTF
- 기울기
- 소프트맥스 함수
- 오차역전파법
- 순전파
- 신경망 학습
- 아파치
- 역전파
- 코딩
- PHP
- flag
- Today
- Total
Story of CowHacker
딥러닝 4.3 오차역전파법 본문
이번 글에서는 먼저 Affine 에대해 알아보겠다.
Affine 계층이란?
신경망의 순전파 때 수행한 행렬의 곱을 기하학에서는 Affine계층이라고 불린다.

그림1을 보면 행렬의 곱에서 대응하는 차원의 원소 수를 일치 시킨다는걸 볼수있다.

그림2 는 Affine계층의 계산 그래프를 나타낸것이다.
X, W, B가 행렬이라는 점에 주의해야한다.
지금까지의 계산 그래프트 노드 사이에 스칼라값이 흘렀는데 이 예에서는 행렬이 흐르고 있다.
이제 그림2의 역전파를 식으로 나타내보겠다

이제 계산그래프로 나타 내보겠다.
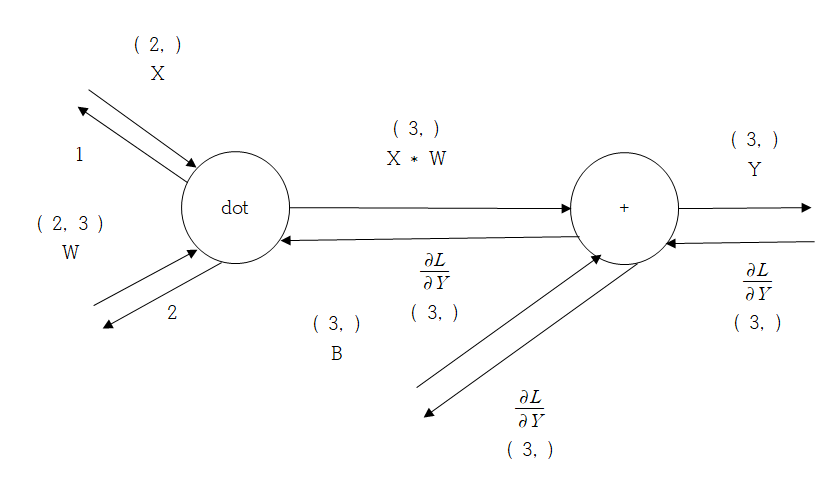
그림4를 보면 1, 2로 표시 된곳이 있는데 그것은 바로
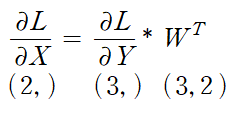

그림5는 1
그림6은 2다.
지금까지 봐온 Affine계층은 입력 데이터로 X 하나만 고려한 것이였다.
이번에는 데이터 N개를 묶어 순전파 하는 경우의 배치용 Affine계층을 알아보겠다.

그림7 에서도 숫자 1, 2, 3 이렇게 표시된곳이 있는데

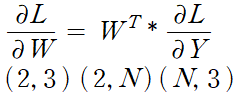

그림 8 ~ 10 까지 순서대로
1, 2, 3을 뜻한다.
이제 이모든것을 파이썬 코드로 구현해볼것이다.
코드는
출처 : https://github.com/WegraLee/deep-learning-from-scratch
WegraLee/deep-learning-from-scratch
『밑바닥부터 시작하는 딥러닝』(한빛미디어, 2017). Contribute to WegraLee/deep-learning-from-scratch development by creating an account on GitHub.
github.com
여기서 받은 파일 common/layers.py에 있다.
Affine코드
import numpy as np
from common.functions import *
from common.util import im2col, col2im
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
# 가중치와 편향 매개변수의 미분
self.dW = None
self.db = None
def forward(self, x):
# 텐서 대응
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 입력 데이터 모양 변경(텐서 대응)
return dx
이까지 Affine계층에 대해 알아봤다.
'공부 > 딥러닝' 카테고리의 다른 글
| 딥러닝 4.5 오차역전파법 (0) | 2020.08.19 |
|---|---|
| 딥러닝 4.4 오차역전파법 (0) | 2020.08.19 |
| 딥러닝 4.2 오차역전파법 (0) | 2020.08.17 |
| 딥러닝 4.1 오차역전파법 (0) | 2020.08.17 |
| 딥러닝 4.0 오차역전파법 (0) | 2020.08.16 |




