| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- flag
- 아파치
- 우분투
- Python Challenge
- sgd
- 소프트맥스 함수
- 역전파
- 리뷰
- PICO CTF
- PostgreSQL
- 순전파
- AdaGrad
- 책
- FastAPI
- Apache2
- 딥러닝
- 설치
- 신경망 학습
- 코딩
- PHP
- 백준
- HTML
- 신경망
- picoCTF
- 오차역전파법
- 기울기
- 파이썬
- CTF
- Python
- C언어
- Today
- Total
Story of CowHacker
딥러닝 3.1 신경망 학습 본문
이번 글에서는 먼저 미분에 대해 알아볼 것이다.
미분 : 특정 순간의 변화량을 뜻한다.

그림 1은 미분을 수식으로 나타낸 것이다.
좌변은 x에 대한 f ( x )의 변화량을 나타내는 기호다.
결국, x의 작은 변화가 함수 f ( x )를 얼마나 변화시키느냐를 의미한다.
이때 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미로 lim h->0로 나타낸다.
이제 위 미분을 파이썬으로 구현해보겠다.
미분 코드
def numerical_diff ( f, x ) :
h = 1e-4
return ( f ( x + h ) - f ( x - h ) ) / ( 2 * h )
함수 이름은 수치 미분을 뜻한다.
이 함수는 함수 f와 함수 f에 넘길 인수 x라는 두 인수를 받는 원리다.
그럼 이제 위 함수를 사용해 간단한 함수를 미분해보겠다.
일단 우리가 미분할 2차 함수를 보겠다.

그림 2가 바로 우리가 미분할 2차 함수다.
이것을 파이썬으로 구현해보겠다.
2차원 함수 코드
def function_1 ( x ) :
return 0.01 * x ** 2 + 0.1 * x
이제 이 2차원 함수 그래프를 그리는 코드를 짜 보겠다.
2차원 그래프 코드
import numpy as num
import matplotlib.pylab as plt
def function_1 ( x ) :
return 0.01 * x ** 2 + 0.1 * x
x = num.arrange ( 0.0, 20.0, 0.1 )
y = function_1 ( x )
plt.xlabel ( "x" )
plt.ylabel ( "f(x)" )
plt.plot ( x, y )
plt.show()

위 코드를 실행시키면 그림 3처럼 2차 함수 그래프가 나온다.
이제 아까 파이썬으로 구현한 수치 미분 함수로 미분을 해볼 것이다.
2차 함수 미분 코드
print ( numerical_diff ( function_1, 5 ) )
print ( numerical_diff ( function_1, 10 ) )
위 코드는 x = 5일 때와 10일 때의 함수를 미분한 것이다.
결과 값은
0.1999999999990898
0.2999999999986347
이렇게 나오는데 한번 그래프를 그려 보겠다.


그림 4는 x 가 5일 때의 접선을 나타 낸 것이다.
그림 5는 x 가 10일 때의 접선을 나타 낸 것이다.
다음은 편미분에 대해서 알아보겠다.
먼저 변수가 2개인 함수 수식을 한 개 보자.

위 수식을 이제 파이썬으로 구현해보겠다.
변수 2개 함수 코드
def function_2 ( x ) :
return x [ 0 ] ** 2 + x [ 1 ] ** 2
편미분이란
위 함수처럼 변수가 여러 개 있는 함수에 대한 미분을 편미분이라고 한다.
그럼 편미분을 수식으로 나타 내보겠다.
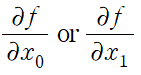
그림 7에 있는 편미분 수식을 이용해 파이썬으로 편미분 문제를 풀어 보겠다.

그림 8 문제를 파이썬 코드를 짜 보겠다.
def numerical_diff ( f, x ) :
h = 1e-4
return ( f ( x + h ) - f ( x - h ) ) / ( 2 * h )
def function_tmp1 ( x0 ):
return x0 * x0 + 4.0 ** 2.0
print ( numerical_diff ( function_tmp1, 3.0 ) )
출력 값 즉, 답은 6.00000000000378이다.
이까지 미분과 편미분을 파이썬 구현을 통해 알아보았다.
'공부 > 딥러닝' 카테고리의 다른 글
| 딥러닝 3.3 신경망 학습 (0) | 2020.08.13 |
|---|---|
| 딥러닝 3.2 신경망 학습 (0) | 2020.08.13 |
| 딥러닝 3.0 신경망 학습 (0) | 2020.08.11 |
| 딥러닝 2.9 신경망 (0) | 2020.08.10 |
| 딥러닝 2.8 신경망 (0) | 2020.08.08 |




