| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Apache2
- picoCTF
- flag
- CTF
- C언어
- sgd
- 아파치
- 신경망
- 책
- AdaGrad
- 오차역전파법
- 역전파
- 딥러닝
- Python Challenge
- 설치
- 소프트맥스 함수
- PostgreSQL
- PICO CTF
- Python
- PHP
- 백준
- 기울기
- 순전파
- FastAPI
- 우분투
- 파이썬
- HTML
- 코딩
- 리뷰
- 신경망 학습
- Today
- Total
Story of CowHacker
딥러닝 3.0 신경망 학습 본문
이제 신경망 학습에 대해 알아보겠다.
먼저 신경망의 특징에 대해 보면 데이터를 보고 학습할 수 있다는 점이다.
이 말은 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 뜻이다.
여기서 신경망의 매개변수의 수는 수천에서 수만입니다.
더 들어가 층을 깊게 한 딥러닝 정도면 수억에 이른다.

그림 1은 이미지 5라는 것을 숫자 5라고 인식하는 과정을 나타낸 것이다.
첫 번째 과정은 사람이 생각한 알고리즘을 토대로 한 과정이다. 가장 어려운 방식이다.
두 번째 과정은 사람이 생각한 특징과 머신러닝을 토대로 한 과정이다.
세 번째 과정은 사람 개입 없이 온전히 신경망을 토대로 한 과정이다.
세 번째 과정을 종단 간 머신러닝 이라고도 한다.
처음부터 끝까지 사람의 개입 없이 결괏값을 얻을 수 있다는 뜻을 가지고 있다.
손실 함수
손실 함수란 신경망 학습에서 신경망 성능의 나쁨을 나타내는 지표다.
손실 함수는 일반적으로 오차 제곱합과 교차 엔트로피 오차를 사용한다.
1) 오차 제곱합 ( SSE )
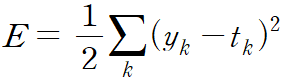
그림 2는 오차 제곱합을 수식으로 나타낸 것이다.
해석을 해보면 yk는 신경망의 출력, tk는 정답 레이블, k는 데이터의 차원수를 나타낸다.
y = [ 0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0 ]
t = [ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0 ]
위 배열중 y는 소프트맥스 함수의 출력이다. 소프트맥스 함수의 출력은 확률로 해석할 수 있었다.
y를 해석해보면 이미지가 0일 확률은 0.1%, 1일 확률은 0.05%, 2일 확률은 0.6%다.
t는 정답을 가리키는 정답 레이블이다.
확률이 제일 높은 0.6%의 자리가 1이고 나머지는 0으로 표현한 걸 알 수 있다.
여기서 자리가 1 인 것의 위치가 2다. 즉 정답이 2 임을 알 수 있다.
t처럼 한 원소만 1로 하고 그 외는 0으로 나타내는 표기법을 원-핫 인코딩이라고 한다.
이제 오차 제곱합을 파이썬으로 구현해보겠다.
오차 제곱합 ( SSE ) 코드
import numpy as num
def sum_squares_error ( y, t ):
return 0.5 * num.sum ( ( y - t ) ** 2 )
위 코드는 오차 제곱합을 파이썬으로 구현한 것인데
각 원소의 출력 ( y )과 정답 레이블 ( t )의 차를 제곱한 후, 그 총합을 구한다.
2) 교차 엔트로피 오차 ( CEE )
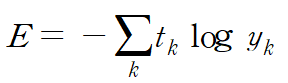
그림 3은 교차 엔트로피 오차를 수식으로 나타낸 것이다.
해석을 해보면 yk는 신경망의 출력, tk는 정답 레이블이다.
또 tk는 정답에 해당하는 인덱스의 원소만 1이고 나머지는 0이다.
교차 엔트로피 오차 ( CEE ) 코드
import numpy as num
def cross_entropy_error ( y , t ):
delta = 1e-7
return -num.sum ( t * num.log ( y + delta ) )
위 코드를 해석해보면 y와 t는 넘 파이 배열이다.
마지막 코드를 보면 num.log를 계산할 때 delta를 더한 것을 볼 수 있는데 이것은 num.log 함수에 0을 입력하면 마이너스 무한대를 뜻하는 -inf가 되어 더 이상 계산을 진행할 수 없는 걸 방지하기 위함이다.
미니 배치 학습
지금 까지 데이터 하나에 대한 손실 함수만 봐왔다.
이제는 모든 데이터 손실 함수의 합을 구하는 방법을 알아볼 것이다.
예를 들어 교차 엔트로피 오차의 수식을 보자.

그림 4는 손실 함수의 합을 구할 때의 교차 엔트로피 오차 수식을 나타낸 것이다.
해석을 해보면 데이터가 N 개라면 tnk는 n번째 데이터의 k번째 값을 의미한다.
ynk는 신경망의 출력, tnk는 정답 레이블이다.
위 수식을 사용할 경우 훈련 데이터가 60,000개나 되는 MNIST 데이터셋의 합을 구하려면 많은 시간이 걸린다.
이것을 보완한 것이 바로 미니 배치 학습 코드다.
미니 배치 학습 코드는 60,000장의 훈련 데이터 중에서 100장을 무작위로 뽑아 그 100장 만을 사용하여 학습하는 것이다.
한번 파이썬으로 구현해보겠다.
미니 배치 학습 코드
import sys, os
sys.path.append ( os.pardir )
import numpy as num
from dataset.mnist import load_mnist
( x_train, t_train ), ( x_test, t_test ) = \
load_mnist ( normalize = True, one_hot_label = True )
print ( x_train.shape )
print ( x_train.shape )
첫 번째 print 결과는 ( 60000, 784 ) 다.
해석하면 훈련 데이터는 60,000개고, 입력 데이터는 784 열인 이미지 데이터다.
두 번째 print 결과는 ( 60,000, 10 ) 다.
해석하면 훈련 데이터는 60,000개고, 정답 레이블은 10줄짜리 데이터다.
이제 정답 레이블에서 무작위로 10장만 빼내는 작업을 파이썬으로 구현해볼 것이다.
정답 레이블 추출 코드
import sys, os
sys.path.append ( os.pardir )
import numpy as num
from dataset.mnist import load_mnist
( x_train, t_train ), ( x_test, t_test ) = \
load_mnist ( normalize = True, one_hot_label = True )
train_size = x_train.shape [ 0 ]
batch_size = 10
batch_mask = num.random.choice ( train_size, batch_size )
x_batch = x_train [ batch_mask ]
t_batch = t_train [ batch_mask ]
print ( num.random.choice ( 60000, 10 ) )
위 코드에서 num.random.choice는 지정한 범위의 수 중에서 무작위로 원하는 개수만 꺼낼 수 있다. 예를 들어 num.random.choice ( 60000, 10 )은 0 이상 60000 미만의 수 중에서 무작위로 10개를 골라낸다는 뜻이다.
그럼 이제 미니 배치 같은 데이터를 지원하는 교차 엔트로피 오차를 구현해보겠다.
def cross_entropy_error ( y, t ):
if y.ndim == 1:
t = t.reshape ( 1, t.size )
y = y.reshape ( 1, y.size )
batch_size = y.shape [ 0 ]
return -num.sum ( t * num.log ( y * num.log ( y + 1e-7 ) ) / batch_size
위 코드를 해석해보면
y는 신경망의 출력, t는 정답 레이블이다.
y가 1차원이라면, 데이터 하나당 교차 엔트로피 오차를 구하는 경우는 reshape 함수로 데이터의 형상을 바꿔준다.
그리고 배치의 크기로 나눠 정규화하고 이미지 1장당 평균의 교차 엔트로피 오차를 계산한다.
왜 손실 함수를 설정하는 것인가?
정확도라는 지표를 안 쓰고 손실 함수를 지표로 쓰는 이유는 매개변수의 미분이 대부분의 장소에서 0이 되기 때문이다.
예를 들어 정확도를 지표를 삼을 때는 계단 함수를 떠올리면 된다.
계단 함수 그래프

계단 함수는 대부분의 장소에서 기울기가 0이다.
한편 손실 함수를 지표로 삼았을 때의 상황은 시그모이드 함수를 떠올리면 된다.
시그모이드 그래프

시그모이드 함수의 기울기는 어느 장소라도 0이 되지 않는 걸 볼 수 있다.
이까지 신경망 학습에서 손실 함수에 대해 알아보았다.
'공부 > 딥러닝' 카테고리의 다른 글
| 딥러닝 3.2 신경망 학습 (0) | 2020.08.13 |
|---|---|
| 딥러닝 3.1 신경망 학습 (0) | 2020.08.12 |
| 딥러닝 2.9 신경망 (0) | 2020.08.10 |
| 딥러닝 2.8 신경망 (0) | 2020.08.08 |
| 딥러닝 2.7 신경망 (0) | 2020.08.06 |



